だいぶ前に確率収束論のことを書いた記事※があって、「確率収束論を麻雀にあてはめるのはおかしい」というのをまとめたんだけれども、かなりの長文なので人によってはわかりにくかったかもしれません。
というわけで、すこし補足するために図を作成しました。加筆して編集しなおそうかとも思いましたが、さらに長文になるのはイヤーンなのでここに別記事としておきます。
※関連記事

↑の記事の「あとがき」で話している部分を図を使用してわかりやすくしたような感じになります。
「大勢の視点であればどこかで収束してる」
という部分です。
大勢の視点なら収束してるけど・・・
例によって麻雀では複雑過ぎるのでコイントスで説明していきます。
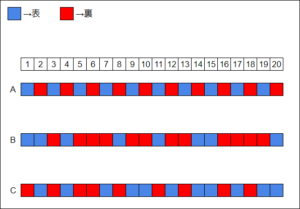
下の図はコイントスの結果を図にしたものです。
青が表、裏が赤、アルファベットは個人を指し、数字は投げた回数を表しています。
A、B、Cの3人が20回ずつコインを投げてその結果を色で分けました。多少のズレはあるもののおおよそ半々の結果になっているかと思います。
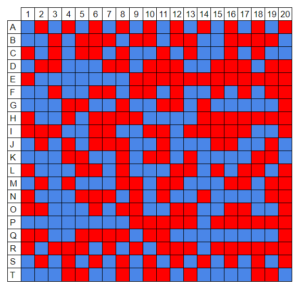
これをさらに人数を増やしたものがこちらの図です。
AさんからTさんまで20名が、それぞれ20回ずつコインを投げた結果を色分けして表しています。
いかがでしょうか?
全体的に見ればおおよそ半々になっていますが、1人1人をよく見ると偏った結果になっている人もいるはずです。
確率収束論を麻雀に当てはめて考えるということは、このうちの一本(つまり自分という視点)がだいたい確率通りの結果になる、ということをあてにした考え方ということになるんです。
でもほら、図を見ればもう明らかですけど、一人の視点なんてこんなもんなんですよ。
確率通りになるかもしれないし、ならないかもしれない。その無限とも言えるほどの無数のパターンが考えられる中で、そのうちのほんの一部分(自分視点)はかたよらないと決めつけているかのようなおかしな考え方なんです。
麻雀の選択(個人、または瞬間的な判断)にはまったく意味が無いと言えます。
また、これは過去、現在、未来、他人の視点もすべて含めて考えることが可能です。それらすべてひっくるめてであれば、確率は収束していると言ってもまったく問題はないでしょう。
その試算回数は膨大なんてもんじゃなくて無限大なんですけどね。
確率計算を元にしている推測データなのだからこれは当然です。
だから「すでに収束してる」と言うことはできます。
でも先に言ったように、個人や瞬間的な判断には使えません。意味ないです。
もし使うのであれば、これは・・・まぁ、あくまでもたとえばの話なんですが。
雀士10000人に「確率の高いほうを選択しろ」と命令できるような場合は、まったく無意味とは言えないかもしれないというのはあります。
確率がどうであれ結果はバラけますので、確率の高いほうを選択した人達のほうが多く結果を出すでしょう。正解の確率が70%でハズレが30%なら、計算上は7000人が当たり、3000人がハズレを引くということですからね。
でもほら、これだと当たった人はいいけどハズレた人はちっとも良くないじゃないですか。
大勢の人に命令できるような立場の人が、少ないほうを犠牲にして多くの好結果を得るという作戦であれば、確率収束論も意味はあるでしょうけれども、やっぱり個人や瞬間的な判断には意味がないですよ。
確率の高いほうを選ぼうが低いほうを選ぼうがその後の振り分けで半々(正解かハズレかの2つに分けた場合)にバラけるわけですから。
麻雀というゲームにおいて確率は大事な要素のうちの一つではありますが、それを最上段に据えるのは明らかな間違いです。
正解がどちらなのかを見極めるために確率を考慮しないということではありません。
ツキや流れ、アヤ牌などを考慮するほうが大事・・・とまでは、私なんかのレベルで言い切ることはできませんけどね(^_^;)
ただ・・・確率の高い方を選ぶ(デジタル※)という打ち方だけをやっていると、どうしてもそこで思考停止することになりますので、ツキや流れなどについての部分は無視することになっちゃいます。
ということは、その方面のスキルがずっと0のままになってしまうんですよねー。
(※現在はデジタル打ちにも色々あるようなので、一括りにはできないかも。ここでは特に確率収束論をあてにしているデジタル打ちの人達ということにしておきます)
無理にツキや流れを信じなくても良いとは思いますけど、確率論だけに執着してしまうとそこからいつまでも抜け出せなくなります。
麻雀が上達していく上でそれはあんまりよろしくないんじゃないかなーと私は思いますけど、そのへんは個人の自由ですのでね。無理にすすめたりする気はありません。
記事をお読みいただきありがとうございました。
おまけ
・個々の結果は他の結果に影響をおよぼすことはありません。表が連続で10回出ても次に裏が出る確率が上がったりはしない。コイントスならば表、裏ともに確率は50%で常に一定。
・1人が1枚を1000回投げようが、100人が1枚を10回ずつ順番に投げようが計算上はまったく同じこと。同時に投げたってそれは同じ。